We present a simplified model of Knot Physics for mathematicians—knot theorists, in particular. This simplified model is intended to be a framework for reasoning about quantum entanglement in this theory.

Knot Physics is a unification theory which assumes that spacetime is a branched 4-manifold embedded in a 6-dimensional space. The branches are braided and intersections of the branches characterize the quantum entanglement. By describing the braided structure of the branches we can describe the quantum entanglement.

Quantum Entanglement in Knot Physics

---

We begin with a brief overview of quantum entanglement in Knot Physics.

Knot Physics assumes that the spacetime manifold is a branched 4-dimensional manifold embedded in a 6-dimensional Minkowski space. Branches of the spacetime manifold can split and recombine.

A particle—like an electron—consists of one particle instance on each branch of spacetime. Each particle instance can move around on its own branch, independently of the particle instances on other branches. These particle instances are a quantum superposition.^[1]

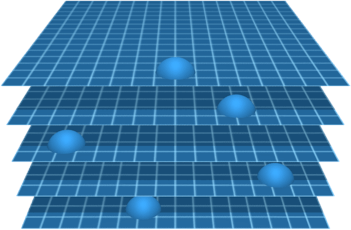
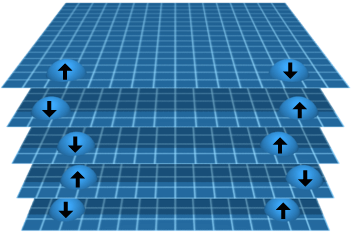
For a given particle, each of its particle instances has its own state, which includes properties like spin. If there are multiple particles, some combinations of particle states may occur with greater or lesser frequency. Entanglement between particles occurs when the branches of spacetime have combinations of particle states that are correlated. (For more on quantum mechanics in Knot Physics, see Theory Summary: Quantum Mechanics.)

Braids on a Simplified Spacetime Manifold

---

We begin by considering a branched 1-dimensional manifold embedded in a 2-dimensional space. This model provides us with the simplest non-trivial notion of branch structure that applies to quantum entanglement.

In this simplified model, we treat particle instances as points on the spacetime manifold and particle properties as abstract labels on those points so that we can more freely examine the structure of the branches.

We assume that each branch \(C_i\) can be described as a function \(f_i : \mathbb{R}^1 \rightarrow \mathbb{R}^1\). Then branches \(C_1\) and \(C_2\) intersect at points \(x\) such that \(f_1(x) = f_2(x)\).^[2]

We begin with two branches \(C_1\) and \(C_2\) and one particle. The particle has one particle instance on each branch. We also include the spin associated with each particle instance.

Our first example consists of two non-intersecting branches and one particle. The branches are \(C_1\) defined by \(f_1(x)=1\) and \(C_2\) defined by \(f_2(x)=-1\), which implies that

\(\{x \mid f_1(x)=f_2(x) \} =\emptyset \).

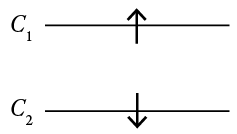
Our second example consists of the same branches and two particles.

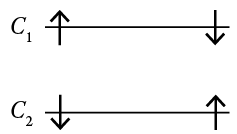
We now consider two intersecting branches and two particles. The branches are \(C_1\) defined by \( f_1(x)=sin(x)+1 \) and \(C_2\) defined by \( f_2(x)=sin(x+ \pi)-1\), which implies that

\( \{ x \mid f_1(x)=f_2(x) \} = \{ \frac{3 \pi}{2}+2 \pi n \} \).

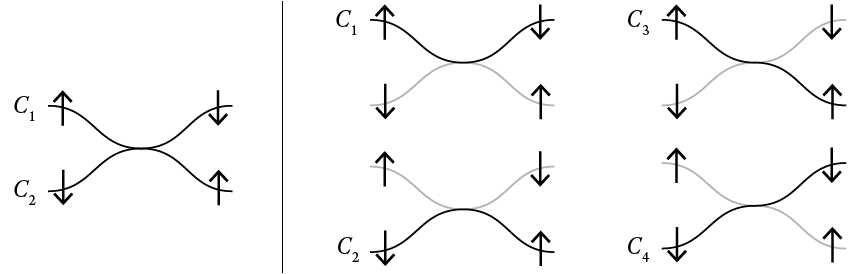
By finding the intersections between branches \(C_1\) and \(C_2\) , we are able to determine the entanglement (or lack of entanglement) between the particle on the left and the particle on the right.

Braids on the Spacetime Manifold

---

Spacetime is a branched 4-dimensional manifold in a 6-dimensional Minkowski space. If we take a constant time slice of spacetime, then we have a branched 3-dimensional manifold in a 5-dimensional space \( \mathbb{R}^5 \). Over small regions, spacetime is approximately flat, and we approximate the branched manifold \(M\) by saying that every branch \(C_i\) of \(M\) is a graph of a map \(f_i: \mathbb{R}^3 \rightarrow \mathbb{R}^2 \):

\(C_i = \{ (x,y,z,f_i(x,y,z)); f_i : \mathbb{R}^3 \rightarrow \mathbb{R}^2 \} \)

\( M = \bigcup\limits_{i} C_i \).

Braids of 2 Branches

Consider two branches \(C_m\) and \(C_n\). Let \(X_{mn}=C_m \cap C_n\). Let \(Y_{mn}= M - X_{mn}\) be the complement of \(X_{mn}\) in \(M\).Let \(Z_{mn}\) be the projection of \(Y_{mn}\) onto \(\mathbb{R}^3\). Then \(f_m \neq f_n\) on \(Z_{mn}\). Let \( x \in Z_{mn} \). An element of the fundamental group \( \pi_1(Z_{mn}, x)\) can be represented by a map \(h:[0,1] \rightarrow Z_{mn}\) such that \(h(0)=h(1)=x\).

The composite maps \(f_m(h(s))\) and \(f_n(h(s))\) are maps from \([0,1]\) to \(\mathbb{R}^2\) such that \(f_m(h(0))=f_m(h(1))\) and \(f_n(h(0))=f_n(h(1))\). In addition, we have that \(f_m(h(s))\neq f_n(h(s))\) for any \(s \in [0,1] \). This implies that the maps \(f_m(h(s)) \) and \(f_n(h(s))\) together are a braid.

Furthermore, \(f_m \neq f_n\) on all of \(Z_{mn}\),which implies there is a homomorphism \(g\) from the fundamental group to the Artin braid group with two strands, \(g:\pi_1(Z_{mn}, x) \rightarrow B_2\).

Braids of More Than 2 Branches

We can perform the same operations on more than two branches. Taking a set \(J\) of \(k\) branches, we can form sets \(X_J\), \(Y_J\), and \(Z_J\).

\(X_J\) is the union of all pairwise intersections of branches in \(J\):

\(X_J= \bigcup\limits_{m, n \in J} C_m \cap C_n \).

\(Y_J=M-X_J\) is the complement of \(X_J\) in \(M\). \(Z_J\) is the projection of \(Y_J\) onto \( \mathbb{R}^3\). Then \(f_m \neq f_n\) for all pairs \(m, n\) on \(Z_J\).

As above, let \(x \in Z_J\), then there is a homomorphism \(g\) from the fundamental group to the Artin braid group with \(k\) strands, \(g: \pi_1(Z_J, x) \rightarrow B_k\).

Physical Properties Following from Manifold Topology

The topology of \(M\) applies to several physically significant properties, including the following:

• The branch intersections characterize the quantum entanglement.
• In Knot Physics, all dynamics result from entropy maximization of the branched spacetime manifold. The topology of the branches is an important part of describing their entropy and therefore the dynamics.
• The spacetime manifold has geometric constraints that may affect branch intersections.
• The elementary fermions of Knot Physics are topological defects, and those topological defects also contribute to the braid structure of the branches.

Notes

---

1. Fermion instances—for example, electron instances—are topological defects in the spacetime manifold of homeomorphism class \(\mathbb{R}^3\#(S^1 \times P^2)\). In other materials, we often refer to these topological defects as “knots” for simplicity.
2. In other materials, we refer to branches as \(B_n\). Only here do we refer to them as \(C_n\) to avoid confusion with notation for braid groups \(B_n\).

Learn More

---