Superfluidity
In Knot Physics, superfluidity results from the properties of the branched spacetime manifold.
Superfluidity
In Knot Physics, superfluidity results from the properties of the branched spacetime manifold.
At 4 kelvin, helium condenses into a liquid with properties similar to water or any other liquid. At 2 kelvin, helium becomes a superfluid with properties unlike any other fluid we can create.
One of the strangest properties of superfluid helium is that it has zero viscosity. A flowing liquid experiences viscosity that causes it to slow down; for instance, stirred coffee eventually stops spinning. Superfluid helium has zero viscosity, and it spontaneously creates vortices that spin without resistance.
In Knot Physics, superfluidity results from the properties of the branched spacetime manifold.
Branched Spacetime
We will describe a few aspects of quantum mechanics in Knot Physics in order to understand superfluidity. (For more on quantum mechanics, see Theory Summary: Quantum Mechanics.)
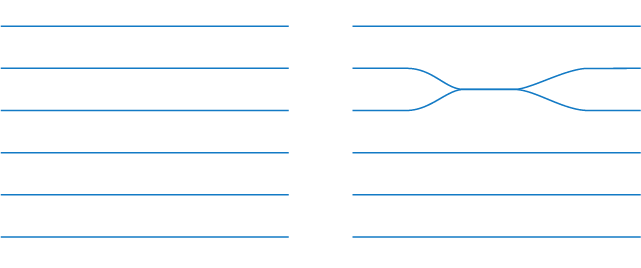
In Knot Physics, spacetime is a branched manifold. The branched spacetime manifold allows a quantum superposition of multiple states, where each branch is a quantum state.
The branches of spacetime split and recombine randomly.
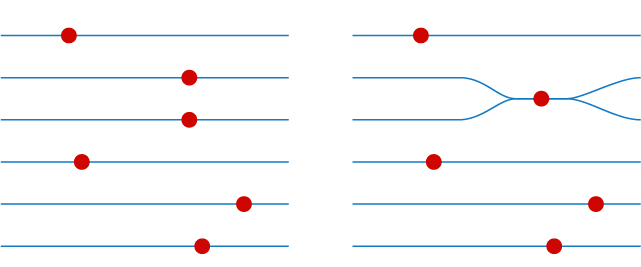
Elementary fermions—like electrons and quarks—are knots in the spacetime manifold. A fermion consists of one knot on each branch of spacetime. All the knots collectively are in a superposition, which is the quantum wave function for the fermion.
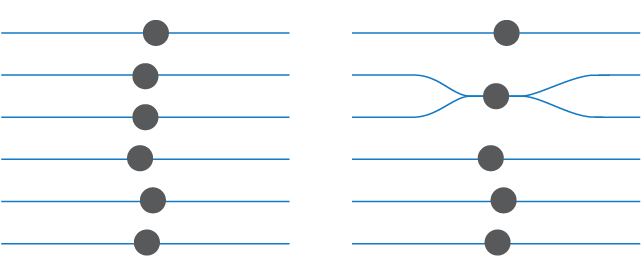
In order for two branches to recombine, the knots on each of the recombining branches must match.
Atoms are made of fermions, so an atom has one “instance” on each branch of spacetime. We refer to each instance of an atom as an atom-instance. In order for two branches to recombine, the atom-instances on each of the recombining branches must match.
If there are \(N\) atoms, then each branch has \(N\) atom-instances.
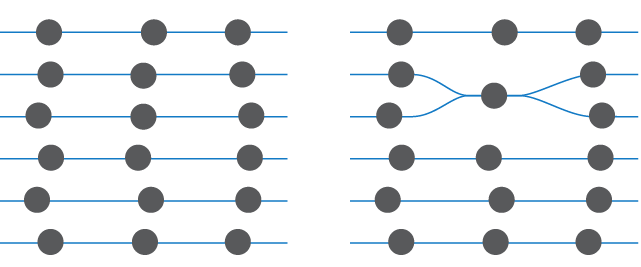
In Knot Physics, the branches of spacetime must frequently recombine. This is because branch recombination has entropy, and the entropy of branch recombination is greatest when the branches recombine frequently.[1] For branches to recombine, the atom-instances must match; specifically, the positions and momenta of the atom-instances on the recombining branches must match.
Superfluidity results from a particular type of flow of atom-instances on the branches of spacetime. In constructing this flow type, we will use the fact that positions and momenta of the atom-instances on the recombining branches must frequently match.
Superfluidity results from a particular type of flow of atom-instances on the branches of spacetime.
Superfluid Flow
Atoms consist of atom-instances on the branches of spacetime. If the atoms are a fluid, then the atom-instances can flow, and the way in which those atom-instances flow is their flow type. We construct a superfluid flow type using three basic flow types. Each basic flow type describes the flow of atom-instances on a single branch.
In the first basic flow type, the atom-instances are at rest with respect to their container.

In the second basic flow type, the atom-instances move with constant velocity relative to their container.

In the third basic flow type, the atom-instances move with a variable velocity. This variable velocity could be described as constant motion plus a longitudinal wave.

We recall that the branches of spacetime must frequently recombine. For branches to recombine, the positions and momenta of the atom-instances on the recombining branches must match.
Clearly the first two basic flow types cannot recombine with each other. The momenta of the atom-instances on those basic flow types never match.

The first basic flow type can, however, recombine with the third. This recombination includes translation such that the third flow type translates relative to the first flow type before the branches recombine.


The third basic flow type can also recombine with the second.

The combination of these three basic flow types is viable because it allows frequent branch recombination. We call this combination the superfluid flow type.

The superfluid flow type has atom-instances that are at rest, atom-instances that are in constant motion, and atom-instances that alternate between those velocities. The superfluid flow type is a quantum superposition that includes a fluid state that is at rest and a fluid state that is in motion.
The superfluid flow type is a quantum superposition that includes a fluid state that is at rest and a fluid state that is in motion.
We now show why the superfluid flow type can only occur at very low temperatures.
Temperature
The superfluid flow type depends on translation of the third flow type relative to the first. By considering the impact of temperature on branch recombination, we can see how translation depends on temperature.
When branches recombine, the positions and momenta of the atom-instances must match. The temperature of atom-instances affects their momenta, but branches can recombine even if the atom-instances are hot. After a branch separates, the momentum of an atom-instance matches the momentum of the atom-instance from which it just separated, allowing branch recombination.

Cold atom-instances can also, of course, recombine in this way.

Cold atom-instances have another mode of recombination that includes translation.

Translation is not possible for hot atom-instances because the momenta of the atom-instances do not match after the translation.

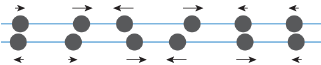
We recall that the superfluid flow type requires translation. Because heat prevents branch recombination of translated branches, it is only possible to construct a superfluid flow type at very low temperatures.
Because heat prevents branch recombination of translated branches, it is only possible to construct a superfluid flow type at very low temperatures.
We now show why the superfluid flow type must have zero viscosity.
Viscosity
Viscosity occurs when the kinetic energy of fluid motion dissipates into the kinetic energy of heat. We can show that the superfluid flow type prevents this kind of energy dissipation.
First, we recall that branches can only recombine if the atom-instances have matching momenta. This means that hot atom-instances cannot recombine with cold atom-instances.

We now consider the three basic flow types that comprise the superfluid flow type: The first flow type has atom-instances at rest, the second has atom-instances with constant velocity, and the third has atom-instances with variable velocity. The first flow type cannot dissipate kinetic energy into heat because the atom-instances are not moving and do not have kinetic energy. Suppose atom-instances in the second or third flow type could dissipate kinetic energy and become hot. The hot atom-instances would no longer be able to recombine with the cold atom-instances of the first flow type. As such, the three branches could no longer frequently recombine with each other.
This never occurs. Entropy of branch recombination requires that branches frequently recombine. As such, the atom-instances of all three basic flow types stay cold in order to frequently recombine with each other. None of the atom-instances can dissipate their kinetic energy of motion into heat, and this means that the superfluid flow type has zero viscosity.
None of the atom-instances can dissipate their kinetic energy of motion into heat, and this means that the superfluid flow type has zero viscosity.
In Knot Physics, superfluidity results from the interaction of different flow types on the branches of the spacetime manifold. By understanding those interactions, we see that the superfluid flow type allows flow but does not allow viscosity. For this reason, a superfluid flows without resistance.

Notes
- To learn more about the effects of branch recombination entropy, see Schrödinger’s Cat.
Image credit: The photograph of superfluid helium is a modified version of an image by Alfred Leitner from the movie "Liquid Helium, Superfluid."
Learn More
Theory Summary
An overview of the entire theory, from simple assumptions about the spacetime manifold through particles, quantum mechanics, and forces
Learn more
Theory Summary
An overview of the entire theory, from simple assumptions about the spacetime manifold through particles, quantum mechanics, and forces
Learn more

