Video Course
Gravity and Quantum Mechanics
This course demonstrates how gravity and quantum mechanics work in Knot Physics. Topics covered include the double slit experiment, virtual particles, and spacetime curvature.
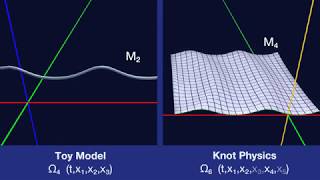
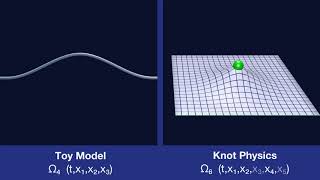
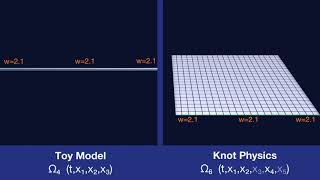
Embedded Manifold
Dimensions
The spacetime manifold is a 4-dimensional manifold embedded in a 5+1 Minkowski space.
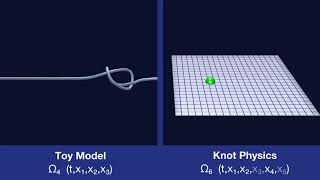
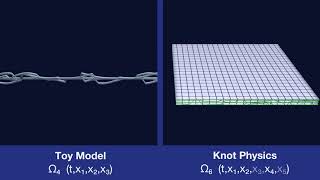
Knots
Knots on Manifolds
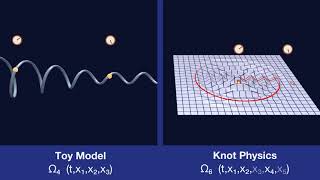
A n-manifold in a n+2-dimensional space can be knotted. Those knots are elementary particles in Knot Physics.
Pair Creation
The knots of Knot Physics are topological defects in the spacetime manifold. Here we show creation of pairs of topological defects on a 2-dimensional manifold. This is analogous to the production of a particle/antiparticle pair.
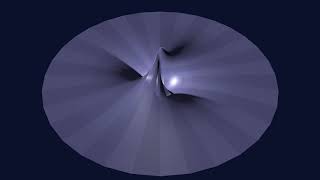
A Topological Defect
We show a closer view of a topological defect on a 2-dimensional manifold. This is a simplified model of the topological defects of Knot Physics.
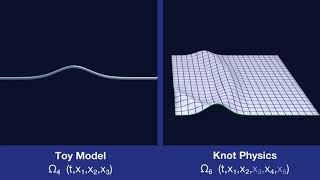
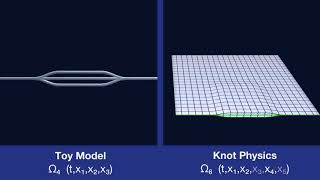
Curvature Constraints
Topologically Flat Spacetime
If spacetime is topologically flat, then the curvature constraints require that the only geometric feature of the manifold is waves.
Geometric Degrees of Freedom
A knot (topological defect) on the spacetime manifold adds geometric degrees of freedom.
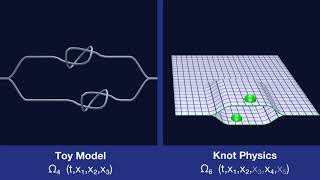
Branches
Branching Examples
In Knot Physics, the spacetime manifold is a branched manifold. Here we show examples of branches that split and recombine. (Geometric separation between branches is exaggerated for clarity.)
Branches and Knots
When branches split and recombine, the knots on the branches also split and recombine.
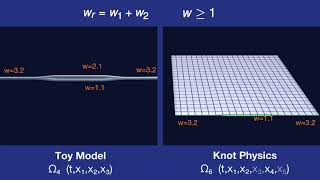
Branch Weight and Branching
There is a branch weight w defined at every point on the spacetime manifold. That weight is conserved at branching.
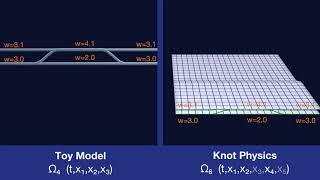
Branch Weight and Geometry
The branch weight w is conserved by stretching of the manifold.
Branch Weight, Branching, and Geometry
The branch weight w is conserved by both branching and stretching. This implies a relationship between branching and stretching.
Dynamics
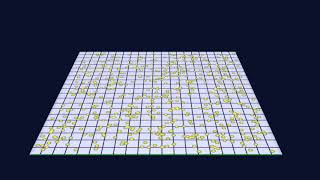
Entropy of Virtual Particles
The spacetime manifold can spontaneously produce virtual particles. These virtual particles contribute to the entropy. (Here we show the production of virtual photons. For more on electromagnetism, please see the papers.)
Entropy of Branching
Recombination of branches of the manifold is random. This recombination contributes to the entropy.
Branch Cohesion
Entropy of branch recombination is reduced when branches are far from each other. For this reason, branches tend to stay close to each other. We call this branch cohesion.
Quantum Mechanics
Knot Amplitude
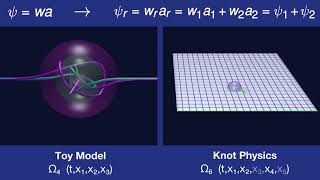
Knots on the spacetime manifold can rotate and change size. We describe this with a single complex number, which we call the knot amplitude.
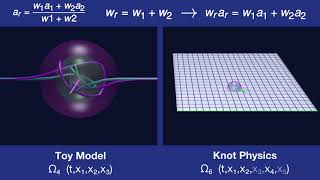
Knot Recombination
When knots recombine, their knot amplitudes recombine to the weighted average amplitude.
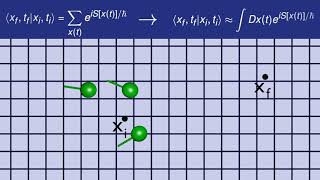
Quantum Path Integral
Using the formula for addition of quantum amplitudes, we derive a formula for summing over the contributions of all knots. In the limit, the formula converges to a path integral.
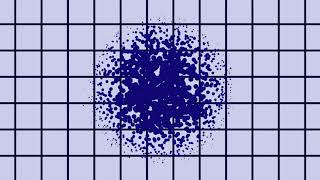
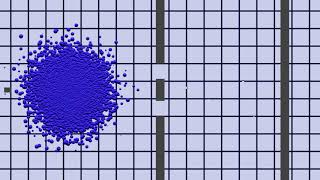
Single Particle Distribution
Using the notion of quantum interference from the path integral, we can demonstrate the behavior of a single real particle. A single real particle has many knots, with one knot on each branch of the manifold.
Gravity
Geometry of Spacetime
We show how an embedded spacetime manifold has geometric characteristics that qualitatively match general relativity.
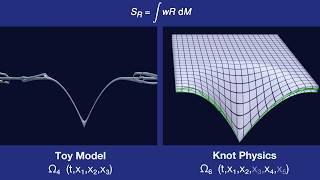
Lagrangian of Curvature
Branch recombination has entropy. Stretching reduces branch recombination. We give a formula relating stretching and entropy. The formula has the form of a Lagrangian.
Lagrangian of Matter
Matter reduces the entropy of the spacetime manifold. We give a formula relating matter and entropy. The formula has the form of a Lagrangian.
Quantum Gravity
We combine spacetime geometry with entropy to produce a Lagrangian that has the form of the Einstein-Hilbert action of general relativity.
Learn More
Theory Summary
An overview of the entire theory, from simple assumptions about the spacetime manifold through particles, quantum mechanics, and forces
Learn more
Theory Summary
An overview of the entire theory, from simple assumptions about the spacetime manifold through particles, quantum mechanics, and forces
Learn more