Electroweak
Knot Physics uses a geometric model of fermions to explain the relationship between electromagnetism and weak force.
Background
The Standard Model
In the Standard Model, electroweak force is a unification of two forces: electromagnetism and weak force.
Electromagnetism
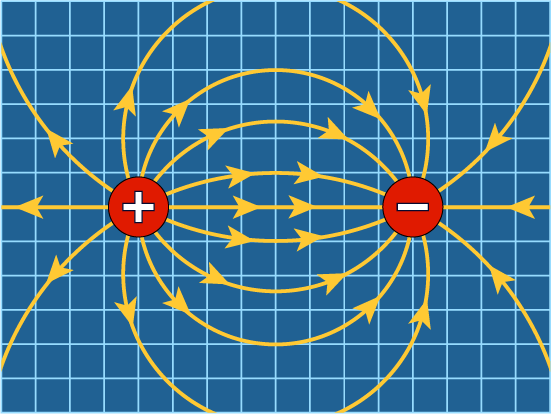
Electromagnetism describes the behavior of the electromagnetic field and charged particles. Changes to the electromagnetic field are propagated by photons, which are massless bosons.
Weak Force
Weak force describes fermion interactions that occur through massive W and Z bosons. For example, a muon (\( \mu^-\)) can decay to a mu neutrino (\( \nu_\mu \)) and a W boson. The W boson then decays to an electron (\( e^-\)) and an electron antineutrino ( \( \overline{\nu_e} \) ). The charge of the muon is carried by the W boson to the electron in the decay process.
In Knot Physics, electroweak unification is a consequence of including fermion geometry in the description of the electromagnetic field.
Electromagnetism
Spacetime has an electromagnetic field.
In Knot Physics, the spacetime manifold is embedded in a larger space. There is an electromagnetic field that is defined on every point of spacetime but not elsewhere in the larger space. Changes to the electromagnetic field propagate as photons.
More detail: The spacetime manifold is a 4-dimensional manifold embedded in a 6-dimensional Minkowski space. Both Knot Physics and the Standard Model have an electromagnetic potential \( A^\nu \) and a corresponding electromagnetic field tensor \( F^{\mu\nu} = A^{\nu,\mu} - A^{\mu,\nu} \) . In both cases the action is proportional to \( F^{\mu\nu}F_{\mu\nu} .\) For more information, see Theory Summary: Electromagnetism.

Fermions are knots in spacetime and can have charge.
The spacetime manifold can be knotted. Knots in spacetime are the elementary fermions—for example, quarks and electrons.
Knots have a topology that can be a source of the electromagnetic field. Knots that are a source of the field are charged fermions.
More detail: An elementary fermion is a topological defect with homeomorphism class \( \mathbb{R}^3 \# (S^1 \times P^2),\) referred to here as a knot. This topology can be a source of the electromagnetic field such that the field cusp is distributed across a torus. For that reason, the electromagnetic field has finite energy. For more information on fermion topology and field energy on fermions see the papers Physics on a Branched Knotted Spacetime Manifold and Deriving the Fine Structure Constant.
Weak Force
On knots, the electromagnetic field has both energy and mass.
The mass of the electromagnetic field is determined by the geometry of spacetime. On flat space, the electromagnetic field has energy but no mass. The geometry of a knot is not parallel to flat spacetime; here, the field has both energy and mass.
More detail: The stress-energy tensor \(T^{\mu\nu}\) is defined at every point on the spacetime manifold, including points that are on a knot. If the knot is in motion, the velocity vector of the knot will be parallel to flat spacetime. Because the knot geometry is not parallel to flat spacetime, the velocity vector of the knot motion may not be in the tangent space of the manifold on the knot. This causes the stress-energy tensor to Lorentz boost with rest mass. For that reason, field energy on a knot has mass. For more information on fermion topology and field energy on fermions see the paper Physics on a Branched Knotted Spacetime Manifold.

Oscillations of the electromagnetic field on a knot propagate as Z bosons.
The Z boson is an oscillation of the electromagnetic field on a knot that leaves the charge unchanged. On a knot, the electromagnetic field has mass; therefore, the Z boson has mass.
Knots can transfer charge with a W boson.
Muon decay is an example of a W boson carrying charge on a knot. The charge of the muon transfers onto the electron via a W boson. The charge moves down the side of the muon knot, which is not parallel to flat spacetime; therefore, the W boson must have mass.
Summary
Knot geometry affects the behavior of the electromagnetic field. On flat
space, the field is massless; on knots, the field is massive. Photons propagate field changes on
flat space and are therefore massless; W and Z bosons propagate field changes on knots and are
therefore massive.
In the Standard Model, the electroweak unification describes the relationship between the photon, W
boson, and Z boson. In Knot Physics, the relationship is a consequence of including knot geometry in
the description of the electromagnetic field.
More Detail: The Gauge Group of Electroweak Unification
In the Standard Model, the electroweak unification describes symmetry breaking using the gauge group \( SU(2) \times U(1).\) This group can be understood as rotations of the Minkowski 6-space that leave components of the electroweak field invariant. More information about the gauge groups of the electroweak unification can be found in the paper Physics on a Branched Knotted Spacetime Manifold.
Learn More
Electroweak
Electroweak unification is a consequence of including knot geometry in the description of the electromagnetic field.
Theory Summary
An overview of the entire theory, from simple assumptions about the spacetime manifold through particles, quantum mechanics, and forces
Learn more
Theory Summary
An overview of the entire theory, from simple assumptions about the spacetime manifold through particles, quantum mechanics, and forces
Learn more